Most research on robot mapping and exploration makes use of powerful computers and expensive sensors, such as scanning laser rangefinders. We are instead studying the mapping and exploration problem for small, inexpensive, "sensing-limited" robots. These robots have short-range sensing that is sparse (low spatial resolution), so that they have only a highly restricted view of the world around them. Nevertheless, it is possible to create maps of unknown environments with sensing-limited robots.

(This is joint work with Wes Huang.)

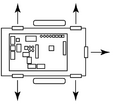robot robot We have developed several algorithms for topological mapping in indoor environments. Topological maps represent the connectivity of the environment, usually in a graph structure where vertices are "distinctive places" in the environment and edges represent paths, classes of paths or behavior sequences for traveling between places.

Our research has mainly investigated single robot topological mapping with sensing-limited robots, addressing issues of exploration strategy, map representation, and loop closure. In the area of multi-robot mapping, we have developed an algorithm for merging topological maps without common reference frames.

Simple single-robot topological mapping

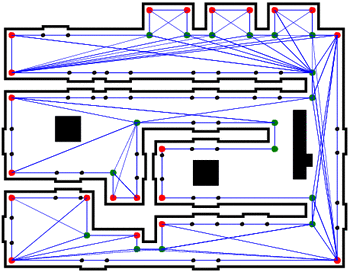map Though not always, many topological maps are augmented with some metric information, such as the lengths of paths (based on the robot's odometry). Our robots keep path length estimates and use an odometry error model to maintain confidence bounds on the estimates.

Our robots create topological maps in which vertices represent specific, "well-defined" features of the environment that are easily detectable even by sensing-limited robots. Typically, these features are significantly-sized corners — interior or exterior — found by the robot as it performs a wall- or hall-following behavior.

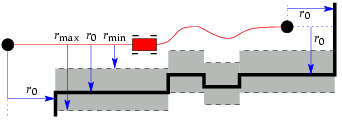wall-following Topological maps generally have difficulty representing "open spaces," i.e., large expanses with few features. In our research, we have addressed this problem in two ways. First, we have introduced the idea of "portals": places where a transition between an open space and an enclosed space occurs. In enclosed spaces (generally corridors in which the robot can see both sides of the hallway), our robots use a hall-following behavior when mapping. In open spaces, they use a wall-following behavior. Second, we have developed the idea of "refinements" to a map created using wall- and hall-following. In open spaces, robots make "forays" through empty areas, adding connections between places in the original map when possible. This can significantly improve navigation efficiency in open areas.

Publications

Wesley H. Huang and Kristopher R. Beevers. Topological mapping with sensing-limited robots. In M. Erdmann et al., editors, Algorithmic Foundations of Robotics VI, pages 235-250, Zeist, Springer, 2005. PDF
Kristopher R. Beevers. Topological mapping and map merging with sensing-limited robots. Master's thesis, Rensselaer Polytechnic Institute, Troy, NY, April 2004. PDF

Loop-closing in topological maps

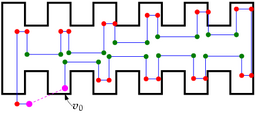loop-closing A difficult problem in mapping is "closing the loop": recognizing when the robot has returned to a place it has already been. We address this with an evidential-reasoning approach based on the Dempster-Shafer theory of evidence. When the map estimate indicates the robot may have returned to a previously-visited place, it "hypothesizes" that it has closed the loop. It then continues to traverse the environment, seeking "evidence" — generally by taking wall-length measurements — that supports or refutes its hypothesis. Eventually, the robot builds enough evidence to accept or reject a particular hypothesis, making its map consistent. Our approach relies on Dempster-Shafer theory to manage loop-closing hypotheses, unlike most approaches which are either probabilistic or heuristic in nature.

Publications

Kristopher R. Beevers and Wesley H. Huang. Loop closing in topological maps. 2005 IEEE International Conference on Robotics and Automation (ICRA 2005), pages 4378-4383, Barcelona, Spain, April 2005. PDF

Topological mapping with the SGVD∞

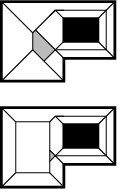
gvd/sgvd sgvd-simulation We have also investigated a topological map representation based on a version of the Generalized Voronoi Diagram (GVD) of the environment. Others have employed the basic GVD as a topological map, with meet points in the GVD as nodes in the map, and edges in the GVD as edges in the map. With an omnidirectional range sensor behaviors can be developed to trace the GVD and build a map. We have again focused instead on the case of more limited sensing — in our model, robots have eight one-dimensional range sensors (e.g., infrared sensors) placed at 45 degree angles around the perimeter of the robot. We have developed behaviors that guarantee complete traversal of the GVD∞ of a rectilinear environment with such robots. (The GVD∞ is similar to the normal GVD, but is defined under the L∞ distance metric instead of the more familiar L2, or Euclidean, metric.)

If the sensors have limited range as well, one can employ the "Saturated" GVD∞, or SGVD∞, which essentially cuts off the GVD∞ at a "saturation distance" corresponding to the maximum range of the sensors. We have developed behaviors for tracing the SGVD∞ as well, and have proved the completeness of the behaviors in the sense that they are guaranteed to explore the entire SGVD∞ of the environment.

Publications

Wesley H. Huang and Kristopher R. Beevers. Complete topological mapping with sparse sensing. Technical Report 05-06, Rensselaer Polytechnic Institute, Troy, NY, March 2005. PDF

Topological map merging

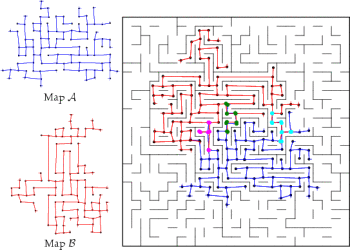matching When multiple robots explore the environment in parallel, it is useful to merge their maps to obtain a global map. This is a difficult problem when the maps lack a common frame of reference.

The approach we have taken to merge topological maps uses aspects of subgraph matching methods to find "structural" matches between map graphs. During this phase of the algorithm, vertices and edges in each map are matched according to their characteristics — both absolute characteristics, such as vertex degree, and approximate characteristics, such as measured path lengths. Structural matching typically reduces the potential matches between the maps to a manageable number.

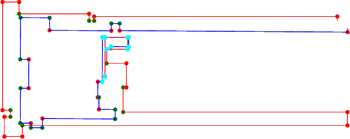Amos Eaton After finding structurally consistent matches between the two maps, we use techniques from image registration methods to find the best transform for each match. The matches are then clustered in transformation space into consistent groups. The best cluster — typically the one with the most vertices and least error — is returned as the hypothesized match between the maps.

We have also introduced data structures for map storage and map update procedures that lend themselves well to this merging strategy.

Our map merging approach has proven very accurate in experiments, and tends to merge maps quickly, usually in well under a second on a Pentium processor — even for maps with hundreds of vertices.

Publications

Wesley H. Huang and Kristopher R. Beevers. Topological map merging. International Journal of Robotics Research, 24(8):601-613, August 2005. PDF
Wesley H. Huang and Kristopher R. Beevers. Topological map merging. In 7th Intl. Symposium on Distributed Autonomous Robotic Systems (DARS 2004), pages 91-100, Toulouse, France, June 2004. PDF
Kristopher R. Beevers. Topological mapping and map merging with sensing-limited robots. Master's thesis, Rensselaer Polytechnic Institute, Troy, NY, April 2004. PDF